Development of High-Strength Microalloyed Coiled Rebar

高強度微合金螺紋盤卷研發

前言---高強度螺紋產品可在混凝土結構中使用小直徑鋼筋，給與混凝土骨料具有較大的空間填充，并且減小了鋼材使用成本。本研究開發 φ20mm 直徑螺紋盤卷，通過添加主要為 Nb 的微合金化元素，生產高強度鋼筋，通過調整軋制工藝參數優化，充分發揮 Nb 元素在冷卻過程的彌散析出。實驗室調研和數學模型指導的工業生產，成功軋制出、了超過 600MPa 強度和超過 15%延伸率的鋼筋。

近年來世界范圍內大型建筑穩步發展，需要大直徑高強高韌的抗震鋼筋，大直徑螺紋盤卷在軋后需要加速冷卻，生產有難度。優化合金設計得到微合金鋼冶金效果，從而生產市場能夠接受可焊接的抗震螺紋鋼筋。

然而，直接研究大直徑熱軋鋼筋是有局限性的，在棒材軋制和軋后冷卻中，要特別考慮軋鋼最高加熱溫度、每個孔型道次高的真應變、較短的恢復再結晶時間（機架之間穿行時間短）、高的應變、有限的軋件冷卻速率。于是，在熱軋這種產品中，出現一些必須考慮的問題，在奧氏體中碳氮化物的脫溶和析出、整個軋制和冷卻中微觀結構再結晶機理、相變中微觀組織結構不同的類型熱軋軋制中的功能（TMP）。常規控制軋制細化晶粒，降低精軋溫度，減少機架間停留時間防止靜態再結晶發生，應變得到積累，導致相變為薄餅組織結構。另一個在熱軋過程中細化晶粒是在較高的軋制溫度下，靜態循環連續變形和亞動態再結晶，能夠產生細小的奧氏體再結晶結構，從而導致相變后鐵素體細小晶粒。

本研究是調研熱軋 φ20mm 螺紋鋼主要的冶金現象，微觀組織結構演變的冶金/數學模型用于預報微合金元素加入量，在工藝上考慮沉淀析出和固溶強化結合，析出的動力學和軋制中線奧氏體晶粒尺寸行為，按照數學/冶金模型指導進行工業試驗，由模型來預報產品的最終的微觀組織和機械性能，冶金模型結合工業試驗結果的屈服強度和延伸率分別超過了 600MPa 和 15%。

1  工業生產過程描述

1.1 軋機布置概況

在本研發中采用熱軋生產線來生產高強高韌螺紋盤卷，步進梁式加熱爐將 155m方坯加熱至 1200℃，加熱后的鑄坯經過除鱗進入 6 機架粗軋機組，而后是 10 機架中軋機組，2 機架預精軋和 10 機架精軋機組。φ20mm 螺紋軋制 18 道次，即 6 機架粗軋機組、8 機架中軋機組、2 道次預精軋和 2 道次精軋。K1~k3 道次（即最后三機架）為圓——橢圓——圓孔型系統。在軋制中采用活套來控制機架間張力，做到無張軋制，具有紅外測溫儀和中間水冷箱，用于控制軋件溫度。在精軋機組前后都設置了水冷箱。臥式吐絲機將鋼筋成圈撒在斯太爾摩線上，斯太爾摩線采用強制風冷，也可轉變為弱冷狀態。本研究中，考慮熱軋參數變化，如溫度、應變、應變速率和道次間隔時間，軋件溫度和時間在線直接量測，應變和應變速率根據孔型和軋制速度計算求得。

1.2  各道次等效應變的計算

原來計算應變使用等效矩型來考慮的，將孔型前后的軋件化為等效面積的矩型，如圖 1 中橢圓孔咬入圓軋件面積為 Ai，將其等面積化為寬度為 Wi 何高度為 Hi 的矩形，于是 Ai=Wi*Hi。同樣經過該道次孔型后的軋件其面積為 Ap=Wp*Hp。

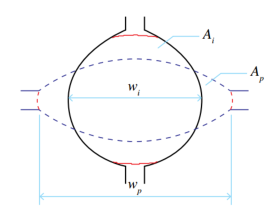
圖 1 圓軋件進入橢圓孔軋制，這里的 Wi 和 Wp 本別是入口軋件寬度和出口軋件寬度，Ai 和 Ap 分別是軋制前后軋件的截面

積

在圓——橢圓孔型系統中，圓面積為 Ai=（π/4）di 2 ，這里 d 是上個道次圓孔型的半徑，而矩形寬度Wi 垂于壓下的方向，這種情況下等于 di，因此 Hi 值為：

Hi =( π4 )di2di= （π/4）di 公式 1

孔型的出口軋件寬度為 Wp，由孔型直接得到Wp 就是等效矩形面積的寬度，其出口軋件面積 Ap 這樣計算

                   Hp =ApWp                     公式 2

這樣就可以計算應變，使用馮.Mises 等效應變的概念，在孔型中的等效應變為

1 ：

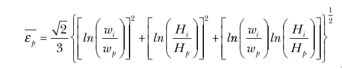
                                                         公式 3

1.3 計算道次的應變速率

由 來定義應變速率，這里的 t c 是接觸時間，給定一個孔型，軋制后等效矩形厚度方向從H i 減少到 H p ，軋輥直徑為 D w ，旋轉速度 NRPM，接觸時間為：

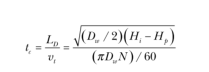
                                             公式 4

這里 D w =D n +S+H p ，D n 是軋輥名義直徑，S 是輥縫，于是，應變速率按下式計算：

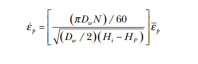
                                               公式 5

1.4  熱機軋制條件

作為給定的軋鋼設備，工藝設計和微合金鋼微觀組織優化需要選擇合適的熱機軋制參數變量，以便在生產中充分發揮能力，做到成本最低。明顯看到，對于每種產品工業設計過程還是有限制因素的，必須考慮軋機剛度和合金設計的經濟性。在本研究工作中，考慮軋制生產線的約束條件，形變熱處理的能力等，見下面：

1、 鑄坯加熱溫度變化范圍為 1000~1200℃之間；

2、 在 13 和 18 道次之間使用水冷箱加速軋件冷卻；

3、 吐絲溫度在 860℃~930℃之間；

4、 斯太爾摩冷卻線散卷冷卻強度在 5~10℃/秒。

2  模型描述

微觀組織結構演變的數學模型，廣泛地用于預報微觀組織細化和最終產品的機械性能，最新的數學模型的構造在軋制螺紋鋼時能預報微觀組織結構的演變，使用一系列公式來描述單獨的冶金過程事件，按照反應的邏輯順序和微觀組織選擇，以便輸入主要的過程參數，模型運算后給出微觀組織結構和機械性能。

表 1 給出使用的數學模型公式。

表 1 模型描述微觀組織結構演變的冶金過程公式

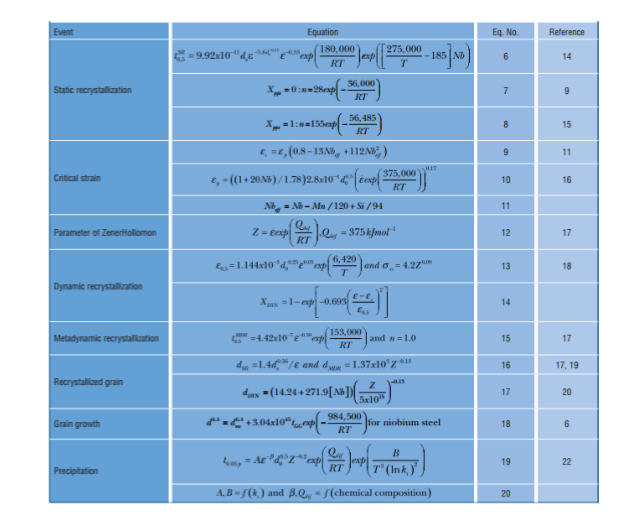
    在第一個道次軋制時，鑄坯是沒有變形應變，應變積累等于該道次的應變計算值，隨后的道次中，在一定的條件下，機架間的再結晶并不完全，導致了應變的積累。于是在這種情況下，前一道次的積累的應變必須加到下一個道次中，由 Gibbs 團隊的公式給出公式7 。然后，作為動態再結晶開始的臨界應變用公式 9~11 計算，為了定義道次之間的軟化類型，不管是動態還是靜態再結晶，考慮軋件重量變化和不同行為的三個區域臨界值，使用 Uranga 團隊提出公式計算8 ：

⚫  區域 I（ε a ＜ε c ）：由靜態再結晶僅僅發生軟化過程

⚫  區域 II（ε c ＜ε a ＜εT）：亞動態和靜態再結晶同時發生

⚫  區域 III（ε a ＞εT）：亞動態再結晶是作用的機理。

當軋件在兩個道次之間通過的時間大于完全軟化發生所需要的時間，模型考慮晶粒長大至到進入下一個道次軋制。在這種情況中，晶粒的靜態和亞動態再結晶要求不同的晶粒長大動能，如公式 18 所示。類似的，以加權的方式計算軋件通過兩個道次之間后的平均晶粒尺寸，正比于間隔時間，正比于兩種機理的最終再結晶比例分數。

靜態和亞動態再結晶動力學由 Avrami 公式計算求得，從表 1 中公式 6 和 15 計算出 50%再結晶時間，Avrami（n）指數變化是作為合金元素函數關系和再結晶自然形成，在微合金鋼中的靜態再結晶情況下不5發生析出，由 Medina 和 Quispe 9 建議，模型考慮 Avrami 指數是軋件溫度的函數關系（公式 7），當析出發生時，靜態再結晶完全停止，一直到析出動力學過程完成。然而，亞動態再結晶過程甚至在應變誘導析出發生10~13 。于是亞動態再結晶，模型考慮 Avrami 指數在析出發生和溫度變化并不改變，假設微合金鋼的這個指為 1.0 不變。當應變誘導析出完成，已經形成的析出相失去了他們的抑制效果，這就允許在靜態再結晶下繼續微觀組織的軟化。然而，析出物存在即使是粗大的，減少了靜態再結晶的動力學條件，公式描述用 n，在 Avrami 公式中時間指數取較保守的公式（公式 8），以便具有較長時間將靜態再結晶過程完成。

模型考慮到應變誘導析出 Nb（C,N）和 VN 的可能性，這兩者析出都具有抑制靜態再結晶的能力，于是使用了由 Medica 團隊研發的應變誘導析出公式22 .公式用于計算開始應變誘導析出是建立在隔熱條件下的，然而，熱軋過程也是一個連續冷卻過程。于是考慮冷卻，作者4,21,23,24 運用了 Scheil 25 添加的原理，應變誘導析出是一個包括形核和長大的現象，允許使用 Avrami 公式闡述它的演變過程：

                                         公式 22

這里 x ppt 是時間 t 析出的分數，n p 是 Avrami 析出指數，t 0.05p 是應變誘導析出開始的時間， Medina 團隊22 建議對于 Nb（C，N）的析出 n p 值為 1.54，對 VN 析出是 2.05。一旦應變誘導析出開始（x ppt ＞0.05），析出分數將添加到軋機之間穿行時間形成析出分數里面，一直到析出動力學完成（Xppt>0.95）。由于 t 0.05p是隨著時間改變的，Avrami 曲線進一步向右移動，延長了時間造成析出領先相變得較為困難。為了補償這個動力學曲線隨著溫度變化產生的位移，Pereda 15 團隊提出引入“添加規則”，運用了等效時間的概念，對不同溫度修正時間，但析出分數保持一個常數。

考慮在溫度范圍的末端 T i 的析出比例分數是 X i ，隨后的溫度 T i+1 間隔末端的析出比例分數首先進行計算，確定等效時間（t eq ）要求達到在溫度 T i+1 之間間隔 X i 析出比例分數數值，這樣在間隔 T i+1 析出分數能這樣計算：

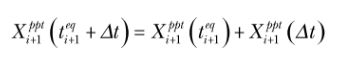
                                             公式 23

這里 t eq 由下式獲得：

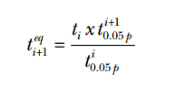
                                         公式 24

于是計算析出分數在每個時間間隔加和，當總和達到 0.95 后完成計算，靜態再結晶過程重新開始計算。用這種方法，模型考慮在塑性變形之后由 Pereda 團隊提出的15 作為再結晶動力學等效時間的概念。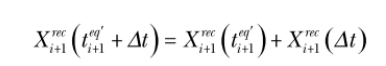

                                                  公式 25

這里 t eq 每個瞬間由下式計算出：

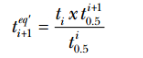公式 26

3  結果

3.1 工業試驗軋制條件

表 2 給出了 Nb 和 V 的化學成分，這里的 C 當量最大為 0.55%，目的是為了保證鋼筋的可焊性。

表 2 使用 Nb 和 V 微合金元素鋼筋的化學成分

表 3 數學模型中 6 種工藝路線

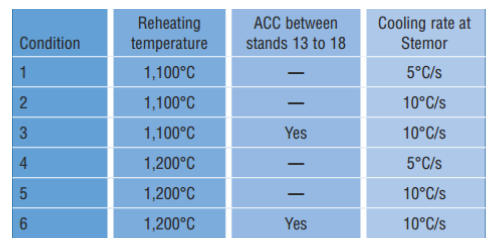
考慮現有軋機所有可能的 TMP 工藝路線，具有 6 種 TMP 軋制模式，見表 3，這些模式和條件是根據微觀組織演變的溫度制度而制定出來的。工藝路線 1~3 的鑄坯加熱溫度為 1100℃，工藝路線 1 是基本工藝條件；2 類似于 1，但是冷卻線發生相變期間的冷卻速率要大，達到 10℃/秒；工藝路線 3 與 2 相同，除了在 13~18 道次采用加速冷卻，使得軋件溫度得到降低；工藝路線 4~6 使用較高的鑄坯加熱溫度（1200℃）；類似于 2 和 3，工藝路線 5 在相變過程采用快速冷卻；6 則同時在 13~18 道次之間采用加速軋件冷卻。

在工藝路線 1~3 中，鑄坯加熱溫度為 1100℃，軋件通過第 1 和第 12 道次溫度在 1087~998℃之間。在工藝路線 1 和 2 中，在軋制中軋件經過 13 和 18 道次溫度范圍在 997℃和 971℃，在工藝路線 3 中，采用加速冷卻，這兩個道次軋件軋制溫度分別為963℃和905℃，在工藝路線4~6中，鑄坯加熱溫度較高到1200℃，在軋件通過第 1 和第 12 道次溫度變化從 1187℃到 1098℃。在工藝路線 4~5 中，通過 13 道次到 18 道次的軋件溫度從1093℃到1070℃，在工藝路線6中，類似于工藝路線3，采用加速冷卻，溫度從1063℃到1048℃。圖 2 表示 6 種工藝路線溫度概況。

圖 2 六種工藝路線軋制過程時間和溫度關系：a 是 1100℃加熱溫度，b 是 1200℃加熱溫度

表 4 選定工藝路線各道次的應變、應變速率和道次間隔時間

表 4 給出了所選定工藝主要輸入參數，等效應變用于所有情況中，在 12、16 和 18 道次上應變較小（0.29,0.28 和 0.32），在 5、7 和 8 道次上用較大的應變（分別為 0.66,062 和 0.63）。所有道次應變的平均值為 0.49，每種工藝路線軋制中用相同的變形速率。應變速率是第 1 道次開始逐漸增加，開始是 1s -1 ，精軋 17 和 18 道次為 130s -1 ，機架之間軋件穿行時間前面長后面短。在粗軋機組到中軋機組之間，預精軋機組到精軋機組之間有較大的距離，目的是增加軋件穿行時間使軋件微觀組織得到充分的軟化。成品軋機到鋼筋在冷卻線上發生相變這段時間最長。

3.2  工業試驗條件下數學模型計算結果

在軋制中一個重要的結果是有多少%Nb 溶解在奧氏體中，鑄坯加熱之后，模型指出在各種的工藝路線中所有的 V 元素（0.110%V）都溶解在奧氏體中。然而，模型指出鑄坯加熱到 1200℃溫度條件下所有的Nb 元素脫溶進入奧氏體中（0.017%Nb），但在鑄坯加熱 1100℃時，只有部分的 Nb（0.010%Nb）脫溶進入奧氏體中。作為析出物的 Nb（C，N），在工藝路線 1~3 中，其析出在第 4 道次之后，對工藝路線 6，析出在 14 道次，在工藝路線 4 和 5，析出在終軋道次上。VN 僅僅在奧氏體中析出，發生在終軋道次和相變前的時間范圍內。作為工藝路線 1~3，在發生相變前溶解在奧氏體中的%Nb 和%V 分別為 0.004%和 0.85%。作為工藝路線 4~6，模型指出溶解在奧氏體中的 Nb 為 0.007 和 0.080%V。圖 3 表明%N 在工藝路線 3 和 6中的演變過程，是軋制時間的函數關系。可以看出 Nb 在固溶體中的量開始下降，就是形成析出物，工藝路線 6 比工藝路線 3 析出時間要晚，也就是在工藝路線 3 中 Nb 在固溶體溶解總是比工藝路線 6 來的低。

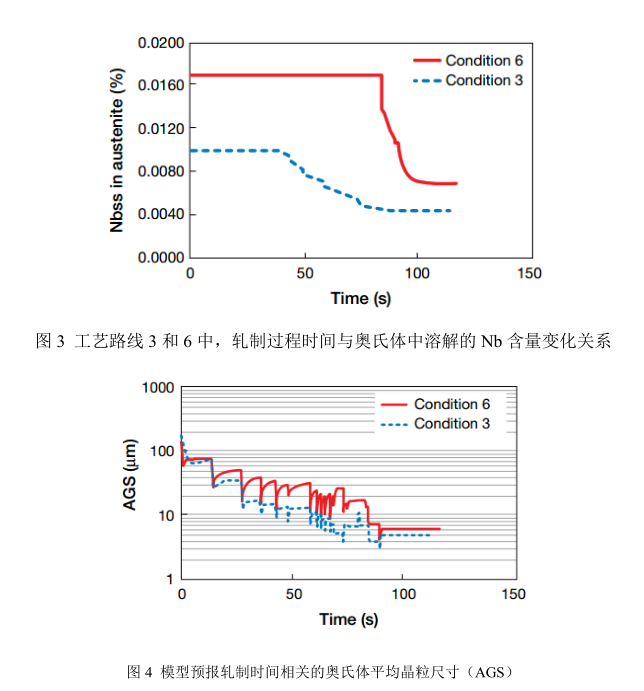
模型也預報奧氏體平均晶粒尺寸（4GS），這與軋制時間均成函數關系，圖 4 給出工藝路線 3 和 6 的一個例子。開始的奧氏體晶粒尺寸為 200μm，然后逐漸減小。工藝路線 6 的熱軋溫度比工藝路線 3 要高，再結晶動力學條件有利晶粒加速長大，結果工藝路線 6 晶粒比工藝路線 3 要粗大，工藝路線 6 中形變誘導析出在第 14 道次，隨著軋制的進程晶粒尺寸顯著減小，到最后工藝路線 6 和 3，晶粒尺寸非常類似。表 5 表示最終 6 種工藝路線的晶粒尺寸。

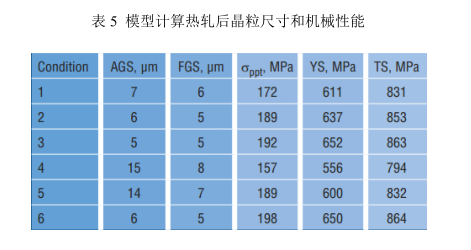
從表 5 可以看到工藝路線不同造成晶粒大小不一，在工藝路線 2、3 和 6 中得到細小的晶粒尺寸，鐵素體晶粒都是 5μm 大小，AGS 發生相變后使得鐵素體晶粒更加細化。鐵素體晶粒大小可以從奧氏體晶粒來預9報的，使用的方法是 Sellars 和 Beynon 提出的公式26 。由于鐵素體析出第二相增加了強度，使用 Hodgaon和 Gibbs 公式計算 δ ppt 2 。這些公式預報出增加的強度正比于相變之前在 r 中溶解的 Nb、V 和 N。作者也提出公式預報屈服強度（YS）和抗張強度（TS）是化學成分、沉淀析出體積分數，和鐵素體晶粒尺寸的函數關系。本研究目標最大的屈服強度，最為有效的工藝路線來增加 YS，使用工藝路線 3 和 6 其 YS 數據達到了 650MPa。

3.3 工業試驗結果

按照模型預報的結果，采用工藝路線 6 進行工業性生產試驗，盡管鑄坯加熱溫度較高，獲得的機械性能與工藝路線 3 類似，但軋制 φ20mm 鋼筋盤卷尺寸控制精確穩定。

圖 5 表明通過最后一個道次棒材的奧氏體微觀組織，可以看到晶粒完全再結晶了，從模型預報 AGS是 6μm，但實際是 9μm。圖 5b 表明獲得的最終微觀組織，主要是鐵素體+珠光體，測量 FGS 是 6μm，與模型預報的 5μm 非常接近。

表 6 表明機械性能、YS 是 620MPa，預報是 650MPa；TS 試驗結果是 850MPa，非常接近與模型預報的 864MPa。強屈比 1.4，延伸率 20%，15%的均勻延伸率是強度和韌性良好地結果，完全適應于抗震鋼筋的主要需求指標。

4 討論

合適的合金設計和優化軋制工藝來生產 φ20mm 直徑的螺紋鋼筋盤卷，屈服強度要達到 600MPa，通常在長材生產中提高強度是采用中碳和較高 V 含量方案，采用這個方案也能達到本文提出的目標。然而，Ceq值要求較低，大約在 0.50%左右，碳含量必須限制，于是只有提高 V 含量要彌補碳含量下降造成的強度不足。作者估計 V 含量要達到 0.19%，N 含量要超過 150ppm，這樣才能達到目標要求，因為提高 V 含量增

加了相變前奧氏體晶粒尺寸，比 Nb—V 鋼粗大，Nb-V 鋼相變前奧氏體晶粒是 5μm，而僅含 V 鋼在相變前是 7μm。看起來奧氏體晶粒相差并非很大，但是在相變后鐵素體晶粒造成了屈服性能上至少有 40MPa 的差別。屈服強度的減少必須增加鐵素體中第二相細小粒子析出來進行補償，于是相比較 Nb-V 鋼，僅僅用V 微合金化鋼筋需要的 V 合金量大，此外，高 V 鋼筋延伸率比 Nb-V 鋼筋要低。

模型預報了將 Nb-V 鋼鑄坯加熱的 1200℃，所有的 Nb（C，N）粒子脫溶，在 1100℃溫度下部分脫溶，VN 在兩種溫度下 V 都進入奧氏體固溶體中。在工藝路線 6 中，足夠的溫度使其所有微合金化元素脫溶進入奧氏體中。在本文中，每個道次的變形相對較高，模型預報出在差不多所有道次中都發生動態和亞動態再結晶，模型指出在道次 1~14 上，靜態、動態、亞動態再結晶混合在一起發生，應變誘導析出 Nb（C，N）從 14 道次之后開始，這個析出完成是在終軋道次到散卷冷卻線相變開始這段時間范圍。這段時間內，VN 也同時析出，析出完成后，奧氏體中的 Nb 和 V 含量分別為 0.007%和 0.080%，這個量在奧氏體中的微合金元素保持量是很重要的，因為在鐵素體冷卻過程中將形成細小彌散強化的第二相析出粒子，第二相粒子析出強度機理貢獻了屈服強度的 30%即 198MPa。最后對比合金成本，單獨用 V 強化需要的合金量大，而使用 Nb-V 合金優化了成本，達到成本和性能組合優勢。

5 結論

本研究主要調查熱軋 φ20mm 螺紋鋼盤卷冶金現象，采用數學模型預報微觀組織的演變過程，加熱和軋制中微合金元素脫溶和析出，預報熱軋過程析出物動力學和 r 晶粒尺寸大小。工業試驗按照模型的指導進行，其結果生產的熱軋螺紋鋼屈服強度超過 600MPa，延伸率超過 15%。

致謝

作者感謝阿賽洛-米塔爾的鼓勵和支持，感謝幫助

                                           2018 年 8 月 5 日翻譯完畢

作者

Roney Lino (top row, left) metallurgical engineer, ArcelorMittal, João Monlevade, MG, Brazil roney.lino@arcelormittal.com.br

Letícia Barbosa (top row, right) metallurgical engineer, ArcelorMittal, João Monlevade, MG, Brazil

leticia.silva1@arcelormittal.com.br

Juscelino Prado (middle row, left) metallurgical engineer, CEFET-MG, Belo Horizonte, MG, Brazil jmpmetalurgica@gmail.com

Felipe Oliveira (middle row, right) metallurgical engineer, ArcelorMittal, João Monlevade, MG, Brazil

felipe.g.oliveira@arcelormittal.com.br

Luciano Reis (bottom row, left) metallurgical engineer, ArcelorMittal, João Monlevade, MG, Brazil

luciano.reis@arcelormittal.com.br

Ronaldo Barbosa (bottom row, right) professor, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brazil

ranmbarbosa@gmail.co

參考文獻

1. Lee, Y., “Calculating Model of Mean Strain in Rod Rolling Process,” ISIJ International, Vol. 39, 1999, p. 961.

2. Hodgson, P.D., and Gibbs, R.K., “A Mathematical Model to Predict the Mechanical Properties of Hot Rolled C-Mn and

Microalloyed Steels,” ISIJ International, Vol. 32, No. 12, September 1992, p. 1329.

3. Maccagno, T.M.; Jonas, J.J.; and Hodgson, P.D., “Spreadsheet Modeling of Grain Size Evolution During Rod Rolling,” ISIJ

nternational, Vol. 36, No. 6, 1996, p. 720.

4. Siciliano, F., and Jonas, J.J., “Mathematical Modeling of the Hot Strip Rolling of Nb Microalloyed Steels,” Ph.D. thesis,

Department of Mining and Metallurgical Engineering, McGill University, Montreal, Que., Canada, 1999, p. 165.

5. Carvalho, R.N., et al., “Evolution of Microstructure of Microliged Steels to Vnb and VNbTi in Continuous Lamination of

Sewing Pipes,” (in Portuguese), Tecnol. Metal. Mater. Miner, Vol. 6, 2009, p. 41.

6. Uranga, P., et al., “Application of Practical Modeling of Microalloyed Steels for Improved Metallurgy, Productivity and Cost

Reduction in Hot Strip Mill Applications,” AISTech 2016 Conference Proceedings, Vol. II, 2016, p. 1769.

7. Gibbs, R.K.; Hodgson, P.D.; and Parker, B.A., Recrystallization (T. Chandra, ed.), Vol. 90, 1990, p. 585.

8. Uranga, P., et al., “Transition Between Static and Metadynamic Recrystallization Kinetics in Coarse Nb Microalloyed Austenite,”

Materials Science and Engineering A, Vol. 345, Nos. 1–2, 2003, p. 319.

9. Medina, S.F., and Quispe, A., “Improved Model for Static Recrystallization Kinetics of Hot Deformed Austenite in Low Alloy and

Nb/V Microalloyed Steels,” ISIJ International. Vol. 41, No. 7, 2001, p. 774.

10. Cho, S.H.; Kang, K.B.; and Jonas, J.J., “The Dynamic, Static and Metadynamic Recrystallization of a Nb-Microalloyed Steel,”

ISIJ International. Vol. 41, No. 1, 2001, p

11. Minami, K., et al., “Mathematical Modeling of the Mean Flow Stress During the Hot Strip Rolling of Nb Steels,” ISIJ

International, Vol. 36, No. 12, September 1996, p. 1507.

12. Siciliano, F., “Mathematical Modeling of the Hot Strip Rolling of Nb Microalloyed Steels,” Ph.D. thesis, Department of Mining

and Metallurgical Engineering, McGill University, Montreal, Que., Canada, 1999, p. 165.

13. Jonas, J.J., “The Hot Strip Mill as an Experimental Tool,” ISIJ International, Vol. 40, No. 8, 2000, p. 731.

14. Fernández, A.I., et al., “Static Recrystallization Behavior of a Wide Range of Austenite Grain Sizes in Microalloyed Steels,” ISIJ

International, Vol. 40, No. 9, 2000, p. 893.

12

15. Pereda, B.; Rodríguez-Ibabe, J.M.; and López, B., “Improved Model of Kinetics of Strain Induced Precipitation and

Microstructure Evolution of Nb Microalloyed Steels During Multi-Pass Rolling,” ISIJ International, Vol. 48, 2008, 10th ed., pp.

1457–1466.

16. Siciliano, F., and Jonas, J.J., “A Mathematical Modeling of Hot Strip Rolling of Microalloyed Nb, Multiply-Alloyed Cr-Mo, and

Plain C-Mn Steels,” Metallurgical and Materials Transactions A, Vol. 31A, No. 2, 2000, p. 511.

17. Roucoules, C.; Yue, S.; and Jonas, J.J., “Effect of Dynamic and Metadynamic Recrystallization on Rolling Load and

Microstructure,” 1st International Conference on Modeling of Metal Rolling Process Proceedings, 1993, p. 165.

18. Senuma, T., et al., Tetsuto-Hagané, Vol. 70, 1984, p. 2112.

19. Abad, R., et al., “Interaction Between Recrystallization and Precipitation During Multi-Pass Rolling in a Low Carbon Niobium

Microalloyed Steel,” ISIJ International, Vol. 41, No. 11, 2001, p. 1373.

20. Ma, L.Q., et al., “Modeling of Dynamic Recrystallization and Flow Stress of Nb-Bearing Steels,” Multidiscipline Modeling in

Mat. and Str., Vol. 3, No. 1, 2007, p. 27.

21. Carvalho, R.N., “Aspects of Precipitation and Recrystallization in Continuous Rolling of Seamless Pipes,” (in Portuguese) Ph.D.

thesis, Metallurgical and Mining Engineering, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brazil, 2007.

22. Medina, S.F.; Quispe, A.; and Gomez, M., “Model for Strain-Induced Precipitation Kinetics in Microalloyed Steels,”

Metallurgical and

Materials Transactions A, Vol. 45A, March 2014, p. 1524.

23. Park, S.H., “Modeling and Measurement of the Continuous-CoolingPrecipitation Kinetics of Nb(C,N) in HSLA Steels,” Ph.D.

thesis, Department of Mining and Metallurgical Engineering, McGill University, Montreal, Que., Canada, 1991, p. 208.

24. Reis, E.G., “Mathematical Model for Predicting Mechanical Properties in Hot Rolling of Structural Profiles,” Metallurgical and

Mining Engineering, Universidade Federal de Minas Gerais, Belo Horizonte, MG, Brazil, 2007.

25. Scheil, E., Arch. Eisenhuttenwes, Vol. 12, 1935, p. 565.

26. Sellars, C.M., and Beynon, J.H., “Microstructural Development During Hot Rolling of Titanium Microalloyed Steels,” D.P.

Dunne and T. Chandra, eds., Conference on High Strength Low Alloy Steels, 1984, p. 142.

唐杰民于 2018 年 8 月上旬翻譯于美國《鋼鐵技術》軋制第 8 期上面的文章，唐工水平不夠，翻譯中出現的種種錯誤和不妥之處請各位給與指正。