摘要：帶鋼懸垂是帶鋼連續處理線中常見的情形，從數學和力學方面對帶鋼懸垂曲線函數和帶鋼張力進行分析，推導出了帶鋼懸垂曲線方程組，同時給出了使用該方程組的2個約束條件。在帶鋼連續處理機組設計時，可以參考使用。

關鍵詞：帶鋼；懸垂曲線方程組；約束條件

1 前言

帶鋼懸垂是帶鋼處理線中常見的情形，對于同一種規格的帶鋼，不同的帶鋼張力對應不同的懸垂曲線。目前對懸垂曲線的形狀尚沒有實用的計算方法，而沒有曲線則不能精確地反映帶鋼張力對支點處的作用力；而且，在帶鋼懸垂段布置與帶鋼高度有關的工藝設備時就難以精確定位。為此，研究了帶鋼張力與懸垂曲線的對應關系，并提出了設計計算方法，為帶鋼連續處理機組的優化設計和控制提供了依據。

2帶鋼懸垂曲線方程組

2．1懸垂曲線函數的建立

為推導懸垂曲線函數，首先建立直角坐標系，如圖1所示。懸垂左支點即帶鋼與轉向輥的切點O為坐標原點(0，0)，實際上該切點的位置是隨帶鋼曲線的變化而變化的，為了方便計算，取轉向輥的最高點為坐標原點；懸垂右支點即帶鋼與轉向輥的切點為Q(x₁，y₂)，同樣，取右端轉向輥的最高點為右支點坐標。設帶鋼的懸垂曲線函數為y=ax² bx c，未知的谷底為P點(x₁，y₁)，懸垂曲線函數表達式為：

2．2懸垂帶鋼長度

對式(1)求導，并在[0，x₂]、[0，x₁]區間內進行積分，得到兩支點間的帶鋼長度l及左支點到谷底P點的帶鋼長度l′：

2．3計算懸垂曲線谷底P點的坐標

對式(1)求導，將懸垂曲線谷底P點的坐標值x₁和y₁代人，得：

2．4左右兩支點的垂直支反力

2．4．1懸垂帶鋼的質量

m=l·g·q，m₁= l′·g·q，m₂=m一m₁(6)式中，m為懸垂帶鋼的質量，kg；l為懸垂帶鋼長度，m；q為單位長度帶鋼質量，kg／m；m₁為左支點O到谷底P的帶鋼質量，kg；l′為左支點O到谷底P懸垂帶鋼長度，m；m₂為谷底P到支點Q的帶鋼質量，kg。

2．4．2帶鋼重心坐標的求解

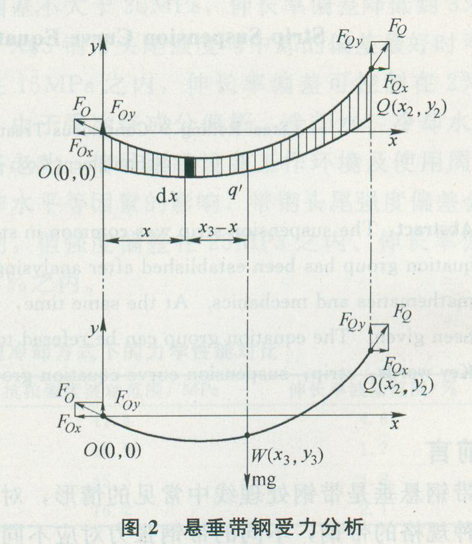
整個帶鋼的重力為mg，其作用點(即重心)為W(x₃，y₃)，如圖2所示。設在帶鋼懸垂態下微段dx上的帶鋼質量為q′，q′與該微段dx處于懸垂曲線上的位置有關，其分布狀況如圖2所示。q′與單位長度帶鋼的質量q的關系為：

q

q′=――――――― (7)

cos(arctan y′)

式中，q′為微段dx上的帶鋼質量，kg／m；q為單位長度的帶鋼質量，kg／m。

因為各微段dx相對帶鋼重點的合面矩為零，所以有：

2．4．3左右支點的垂直支反力

為了簡化思路，設定帶鋼不產生抵抗彎矩，即帶鋼本身的抵抗彎矩為0，因此有：

F_Oy·g·x₂=mg·g·(x₂一x₃)

F_Qy·g·x₂=mg·x₃ (10)

將式(9)代人式(10)有：

F_Oy=m_l g，F_Qy=m₂g (11)

上述式中，F_Oy、F_Qy分別為帶鋼左、右支點的垂直支反力，N。

2．5 帶鋼張力

當兩端支點位置固定后，帶鋼兩端張力和帶鋼單位質量決定著曲線形狀，帶鋼兩端張力的方向是沿帶鋼的切線方向，兩端支點上的垂直支反力實質上是帶鋼張力在垂直方向上的分量。因此：

F_O=F_Oy／y′_O (12)

y′_O為帶鋼左支點切線的斜率，y′_O=dy/dx=b。

所以 Fo=F_Oy／b=m₁ g／b (13)

同理 F_Q=m₂ggx₂／(2y₂一bx₂) (14)

上述式中，F_O、F_Q分別為左、右支點處帶鋼的張力，N；b為帶鋼懸垂曲線函數中無因次量參數。

2．6左右支點同高的帶鋼懸垂曲線方程

當左右支點高度一致，此時Q點坐標為(x₂，0)，將該坐標值代入以上各式，即可求出帶鋼懸垂曲線方程。

3 帶鋼懸垂模型使用的兩個約束條件

前面推導模型的基礎是假設帶鋼不產生抵抗彎矩，而實際情況并非如此，任何一種帶鋼只要存在斷面和材料強度，必然存在固有的抵抗彎矩。但是，對于兩端等高且沒有水平張力的帶鋼(簡稱自由帶鋼)，在帶鋼谷底處，當帶鋼自重產生的彎矩使帶鋼發生彈性變形，隨著兩支點距離的增大，懸垂帶鋼谷底處變形將越來越大。因此不難理解，帶鋼懸垂模型適用范圍的約束條件應該是自由帶鋼發生的變形程度，反之，當帶鋼左右兩支點距離小到一定范圍時，帶鋼自重在帶鋼谷底處產生彎矩小于帶鋼抵抗彎矩，則此時帶鋼的受力情形就變成了梁的變形行為。

3．1 帶鋼的變形曲率極限

純彎曲時帶鋼的縱向纖維發生彎曲，如圖3所示，根據帶鋼的幾何變形方程得：

H

ε_t=±—－

2ρ

(15)

式中，ρ為在懸垂帶鋼谷底處帶鋼中性面的曲率半徑，m；H為帶鋼厚度，m．ε_t為帶鋼表面的彈性應變值。

根據虎克定律有ε_t=σ_t／E，代入式(15)得：

1 2σ_t

—=±------ (16)

ρ HE

式中，σ_t為彈性應力，MPa；E為材料的彈性模量，MPa。

從數學可知懸垂帶鋼曲率幾何方程，并且在谷底處y′=0，因此帶鋼幾何曲率為：

1 y″

——=±—————— (17)

ρ_幾何 (1 (y′)²)^3/2

根據前面的分析，在懸垂帶鋼谷底處帶鋼自重產生的彎矩要大于帶鋼的抵抗彎矩，此處的幾何曲率就必須大于力學曲率，因此將式(16)和式(17)聯立得不等式：

2σ_t

y”≥—— (18)

HE

對式(1)進行2次求導，并代入式(18)，得：

2(y₂－bx₂) 2σ_t

————————≥—— (19)

X₂ HE

對于自由帶鋼，y₂=y_O=0，整理后得：

σ_t

b≤－ ----- (20)

HE

設帶鋼表面的彈性變形應力σ_t和材料的屈服強度σ_s的比值為φ，因此有：

φσ_s

b≤— ――――― (21)

HE

式(21)表明，在求解帶鋼懸垂曲線方程組時，b必須小于0。

3．2懸垂谷底的帶鋼極限彎矩

帶鋼自重在帶鋼谷底產生最大彎矩，當此處帶鋼表面的彎曲應力超過材料屈服強度時，帶鋼自重產生的彎矩將大于帶鋼的抵抗彎矩，可得：

式中，L’為懸垂帶鋼最小跨度，m；H為帶鋼厚度；σ_s為帶鋼屈服強度，MPa。

式(22)表明，在求解帶鋼懸垂曲線方程組時，x₂≥L′。

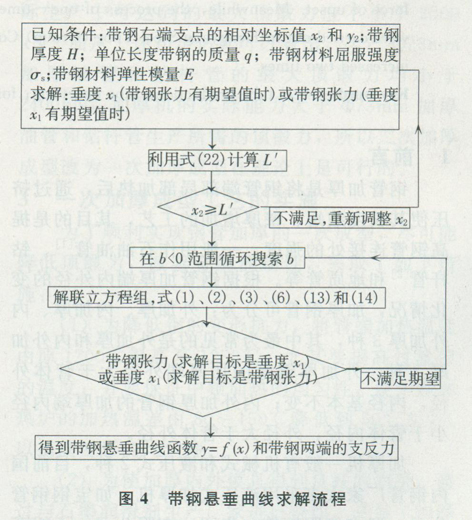
綜上所述，帶鋼懸垂曲線的求解如圖4所示。

4 結論

(1)建立了帶鋼懸垂曲線方程，確定了帶鋼張力與帶鋼懸垂曲線的關系。

(2)給出了帶鋼懸垂曲線方程的2個約束條件，滿足該約束條件，帶鋼懸垂曲線方程可用于工程設計。